분류 전체보기
-
[Unity] bank(fsb)파일에서의 음원(소리) 추출2023.01.19
-
[Unity] 빠른 Play mode 시작2023.01.15
-
[WSL] 재실행 시 nameserver 초기화되는 문제 해결2022.04.07
-
[WSL] 인터넷 연결 안됨 오류2022.04.06
-
리버싱 참고자료(참고도서)2022.03.17
-
[C++] boj 17299 오등큰수2022.03.17
-
[C++] boj 2631 줄 세우기2022.03.08
[Unity] bank(fsb)파일에서의 음원(소리) 추출
bank파일로부터 fsb파일을 분리하고, 다시 fsb파일에서 음원을 추출할 수 있다.
1. 먼저 quickbms를 실행해 같은 폴더에 위치한 Script.bms를 적용한다.

2. 추출할 bank파일이 위치한 폴더 또는 bank파일을 지정한다.
3. fsb 파일이 저장될 폴더를 지정한다.

4. 추출된 fsb파일을 fsb_aud_extr로 드래그해 음원을 추출한다.

이후 아래와 같이 fsb파일의 경로에 음원이추출된다.

'프로그래밍 > Unity' 카테고리의 다른 글
| [Unity] 빠른 Play mode 시작 (0) | 2023.01.15 |
|---|
[Unity] 빠른 Play mode 시작
플레이 모드로 빠르게 접근하는 방법입니다.
제 채널은 아니지만 유튜브 링크를 먼저 소개합니다.
https://www.youtube.com/watch?v=CbbLKGsmG7U&ab_channel=TurboMakesGames
영상을 보기 싫으신 분을 위한 설명은 다음과 같습니다.
1. [Edit] - [Project Settings]에 진입합니다.

2. [Editor] 탭을 선택하고, 아래에서 [Enter Play Mode Settings]를 찾아서 [Enter Play Mode Options]를 체크합니다.

완성! 이제 Play mode에 빠르게 진입합니다.
'프로그래밍 > Unity' 카테고리의 다른 글
| [Unity] bank(fsb)파일에서의 음원(소리) 추출 (0) | 2023.01.19 |
|---|
[WSL] 재실행 시 nameserver 초기화되는 문제 해결
WSL은 왜 설정을 자기 맘대로 초기화하는지 모르겠는데...
sudo apt-get install resolvconf
이후
sudo vi /etc/resolvconf/resolv.conf.d/head

유지할 nameserver 주소를 적고 저장합니다.
sudo service resolvconf --force-reload
이유는 모르겠는데 저는 이거까지 한 번 더 해야 했습니다 왜지?
'기타 > (*) 문제해결' 카테고리의 다른 글
| [WSL] 인터넷 연결 안됨 오류 (0) | 2022.04.06 |
|---|
[WSL] 인터넷 연결 안됨 오류
WSL에서 인터넷이 연결되지 않길래 해결책을 검색해 보았는데,
sudo nano /etc/resolv.conf
이후 기존의 nameserver를 주석처리하고(#),
nameserver 8.8.8.8을 작성하자 정상적으로 작동하였다.

'기타 > (*) 문제해결' 카테고리의 다른 글
| [WSL] 재실행 시 nameserver 초기화되는 문제 해결 (0) | 2022.04.07 |
|---|
리버싱 참고자료(참고도서)
무엇을 학습하려고 하든간에, 매체 없이는 학습하기가 쉽지 않습니다.
도움이 될 수 있는 도서를 소개합니다.
저도 읽어봐야 해서 어느 도서가 가장 많은 도움을 주는지는 잘 모르겠습니다. ㅜㅜ
미래의 제가 서평을 남길겁니다 아마도...
'리버싱' 카테고리의 다른 글
| VaZoNeZ's CrackMe #1 다운로드 및 풀이 (0) | 2022.02.21 |
|---|---|
| ReWrit's Crackme#1 다운로드 및 풀이 (0) | 2022.02.21 |
| dnSpy 다운로드 방법 (0) | 2022.02.18 |
| x96dbg(x64dbg/x32dbg) 다운로드 방법 및 단축키 (0) | 2022.02.16 |
[C++] boj 17299 오등큰수
https://www.acmicpc.net/problem/17299
17299번: 오등큰수
첫째 줄에 수열 A의 크기 N (1 ≤ N ≤ 1,000,000)이 주어진다. 둘째에 수열 A의 원소 A1, A2, ..., AN (1 ≤ Ai ≤ 1,000,000)이 주어진다.
www.acmicpc.net
어떤 수열 A = A1, A2, ..., AN에 대해 각 원소 Ai의 오등큰수 NGF(Ai)를 구하려고 합니다.
수열 A에서 각 원소 Ai가 등장한 횟수가 F(Ai)라고 하니,
먼저 F(Ai)를 구한 뒤에 NGF(Ai)를 구할 수 있겠습니다.
|
1
2
3
4
5
6
7
8
9
|
int N;
cin >> N;
int* A = new int[N];
int* F = new int[1000001]{ 0, };
for (int i = 0; i < N; i++) {
cin >> A[i];
F[A[i]] += 1;
}
|
cs |
그럼 구해야죠.
NGF(Ai)는 수열상에서 Ai보다 오른쪽에 있으면서 수열에서의 등장횟수가 F(Ai)보다 큰, 가장 왼쪽의 수입니다.
여러가지 생각을 해봅니다. 주어진 예제대로 푼다면,
A = [1, 1, 2, 3, 4, 2, 1]일 때 오등큰수는 순서대로 다음과 같이 구해집니다.
NGF = [?, ?, ?, ?, ?, ?, -1] (A6의 오등큰수가 없으므로, -1이 선택됩니다.)
NGF = [?, ?, ?, ?, ?, 1, -1] (A5의 오등큰수는 F(A6)>F(A5)이므로 A6이 됩니다.)
NGF = [?, ?, ?, ?, 2, 1, -1] (A4의 오등큰수는 F(A5)>F(A4)이므로 A5가 됩니다.)
NGF = [?, ?, ?, 2, 2, 1, -1] (A3의 오등큰수는 F(A5)>F(A3)이므로 A5가 됩니다. F(A4)=F(A3)이므로 무시됩니다.)
NGF = [?, ?, 1, 2, 2, 1, -1] (A2의 오등큰수는 F(A6)>F(A2)이므로 A6이 됩니다.)
NGF = [?, -1, 1, 2, 2, 1, -1] (A1의 오등큰수가 없으므로, -1이 선택됩니다.)
NGF = [-1, -1, 1, 2, 2, 1, -1] (A0의 오등큰수가 없으므로, -1이 선택됩니다.)
오른쪽에서부터 오등큰수를 구하면 된다는 생각을 먼저 하게 됩니다.
NGF(6)을 구할 때는 고려할 수가 없고,
NGF(5)를 구할 때는 F(6)을 고려해야 하고,
NGF(4)를 구할 때는 F(5)-F(6)을 고려해야 하고,
NGF(3)을 구할 때는 F(4)-F(6)을 고려해야 하고,
...
즉 오른쪽에서 NGF를 하나씩 구하면서, 고려해야 할 값이 하나씩 늘고 있습니다.
그런데 반드시 고려하지 않아도 될 값이 생기기 마련입니다. 중복된 값일 수도 있고, 가장 큰 수라서 그럴 수도 있죠.
오등큰수를 구하기 위해 체계적인 절차가 필요한데,
이를 스택을 통해 구현하기로 합니다.
많은 자료구조 중 스택을 선택해야 하는 이유는 다음과 같습니다.
1. 오른쪽에서부터 고려 대상인 수를 하나씩 push해야 합니다.
2. 가장 마지막에 push된 값과 비교를 하려면, 스택이 용이합니다. (top()과 비교)
3. push된 원소 중 필요 없는 것을 걸러도 되는 이유가 있습니다.
3번의 예를 봅시다. A = [1, 1, 2, 3, 4, 2, 1]에 대해서 오등큰수를 구하는데,
스택을 통해 오등큰수를 계산한다고 생각해봅니다.
먼저 스택이 비어있다면(비교할 대상이 없다면) 오등큰수는 -1로 설정되어야 할 것입니다.
|
1
2
3
4
5
6
|
stack<int> S;
int* ans = new int[N]{0, };
if (S.empty()) {
ans[i] = -1;
}
|
cs |
오른쪽에서부터 반복문을 이용해 오등큰수를 설정할 것인데,
스택이 비어있지 않다면 비교할 대상이 있는 것이고, 조건과 맞지 않는 원소를 제거합니다.
|
1
2
3
4
5
6
7
8
9
10
11
12
|
stack<int> S;
int* ans = new int[N]{0, };
for (int i = N - 1; i >= 0; i--) {
while (!S.empty() && F[S.top()] <= F[A[i]]) {
S.pop();
}
if (S.empty()) {
ans[i] = -1;
}
}
|
cs |
조건에 부합하지 않는 원소는 이미 제거된 상태이므로,
남은 원소가 있다면 오등큰수를 스택의 최상위 값으로 설정합니다.
그리고, 현재 수를 비교 대상에 넣기 위해 스택에 넣습니다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
stack<int> S;
int* ans = new int[N]{0, };
for (int i = N - 1; i >= 0; i--) {
while (!S.empty() && F[S.top()] <= F[A[i]]) {
S.pop();
}
if (S.empty()) {
ans[i] = -1;
}
else {
ans[i] = S.top();
}
S.push(A[i]);
}
|
cs |
이 방법이 성립하는 이유는 다음과 같습니다.
1. Ai의 오른쪽에 있는 원소가 스택에 비교 대상으로 저장됩니다.
2. 그 중 조건에 일치하지 않는 원소는 지워집니다.
3. 조건에 일치하는 원소는 남았으므로, 오등큰수가 결정됩니다.
4. 조건에 일치하지 않는 원소를 지우고 Ai를 스택에 넣는 과정에서, F[Ai]가 지워진 원소의 F[element] 이상의 값을 가짐이 보장됩니다.
5. 따라서, A[i-1] 등 Ai 이전의 원소와 다음 비교를 수행함에 있어 오등큰수의 결정이 유효해집니다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
|
#include <iostream>
#include <stack>
using namespace std;
int main(void) {
ios::sync_with_stdio(false);
cin.tie(NULL);
int N;
cin >> N;
int* A = new int[N];
int* F = new int[1000001]{ 0, };
for (int i = 0; i < N; i++) {
cin >> A[i];
F[A[i]] += 1;
}
stack<int> S;
int* ans = new int[N]{0, };
for (int i = N - 1; i >= 0; i--) {
while (!S.empty() && F[S.top()] <= F[A[i]]) {
S.pop();
}
if (S.empty()) {
ans[i] = -1;
}
else {
ans[i] = S.top();
}
S.push(A[i]);
}
for (int i = 0; i < N; i++) {
cout << ans[i] << " ";
}
cout << "\n";
return 0;
}
|
cs |
따라서 이렇게 풀이하면 되겠습니다.
'ps > acmicpc.net' 카테고리의 다른 글
| [C++] boj 2631 줄 세우기 (0) | 2022.03.08 |
|---|---|
| [Python 3] boj 2579 계단 오르기 (0) | 2022.02.17 |
[알고리즘] [C++] 순열(Permutation)과 조합(Combination)
가끔 순열 또는 조합을 사용해야 할 일이 있습니다.
모든 경우에 대해 브루트 포스(Brute-Force) 방식으로 접근을 시도할 때 더욱이 많이 사용하곤 하는데요,
순열(Permutation)은 순서가 정해져 있는 나열이고
조합(Combination)은 순서를 고려하지 않고 고른 것을 말합니다.
예를 들어 1, 2, 3에 대한 순열은 다음과 같습니다.
123
132
213
231
312
321
1, 2, 3에 대한 조합은 다음과 같습니다.
123
사실 조합은 여러 개 중 일부를 택할 때 의미가 있습니다. 그러니 1, 2, 3, 4 중 세 개를 택한 조합을 나열해보면,
123
124
134
234
이렇게 네 가지가 되겠습니다.
C++에서의 algorithm 헤더는 next_permutation과 prev_permutation을 지원합니다.
오름차순으로 정렬된 데이터는 next_permutation을 통해,
내림차순으로 정렬된 데이터는 prev_permutation을 통해 순열을 구할 수 있습니다.
|
1
2
3
4
5
6
7
8
9
10
11
|
string token = "123";
do {
cout << token << "\n";
} while (next_permutation(token.begin(), token.end()));
cout << "----\n";
token = "321";
do {
cout << token << "\n";
} while (prev_permutation(token.begin(), token.end()));
|
cs |
실행 결과는 다음과 같습니다.
123
132
213
231
312
321
---
321
312
231
213
132
123
그럼 이제 조합을 알아볼 차례입니다.
조합 역시 순열을 약간 응용해서 구현할 수 있는데,
prev_permutation을 이용한 방법은 이렇게 설명할 수 있습니다.
1. 주어진 token에 대응할 flag를 만듭니다.
2. 그 flag에 원하는 자릿수만큼 true를 채우고, flag에 prev_permutation을 사용해 전체 순열을 대상으로 동작할 수 있게 합니다.
3. 매 loop에서 flag가 true인 부분만 출력합니다.
즉, 전체 가짓수에서 원하는 개수만큼만 뽑는다고 할 수 있습니다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
string token = "12345";
for (int i = 0; i < 5; i++) {
vector<bool> flag(token.length(), false);
for (int j = 0; j <= i; j++) {
flag[j] = true;
}
do {
for (int j = 0; j < token.length(); j++) {
if (flag[j]) cout << token[j] << " ";
}
cout << "\n";
} while (prev_permutation(flag.begin(), flag.end()));
}
|
cs |
실행 결과는 다음과 같습니다.
1
2
3
4
5
1 2
1 3
1 4
1 5
2 3
2 4
2 5
3 4
3 5
4 5
1 2 3
1 2 4
1 2 5
1 3 4
1 3 5
1 4 5
2 3 4
2 3 5
2 4 5
3 4 5
1 2 3 4
1 2 3 5
1 2 4 5
1 3 4 5
2 3 4 5
1 2 3 4 5
이제 순열과 조합을 사용해 볼 수 있겠습니다. 잘 됐네 잘 됐어
'알고리즘 > 알고리즘' 카테고리의 다른 글
| [알고리즘] 가장 긴 증가하는 부분 수열(LIS, Longest Increasing Subsequence) (0) | 2022.03.08 |
|---|---|
| [알고리즘] 이진 탐색 / 이분 탐색 (Binary Search) (0) | 2022.02.24 |
| [알고리즘] 재귀(Recursion)와 꼬리 재귀(Tail Recursion) (0) | 2022.02.22 |
| [C++] 입출력 속도 개선, ios::sync_with_stdio(false) (0) | 2022.02.20 |
[C++] boj 2631 줄 세우기
https://www.acmicpc.net/problem/2631
2631번: 줄세우기
KOI 어린이집에는 N명의 아이들이 있다. 오늘은 소풍을 가는 날이다. 선생님은 1번부터 N번까지 번호가 적혀있는 번호표를 아이들의 가슴에 붙여주었다. 선생님은 아이들을 효과적으로 보호하기
www.acmicpc.net
줄 세우기가 만연한 우리 사회 속에서 어떻게 해야 줄을 잘 세울 수 있을지를 탐구해보는 문제입니다.
어린이집에 N명의 아이들이 있는데, 선 순서가 무작위입니다.
옮길 아이를 최소로 해서 다시 정렬된 상태가 되게끔 하고 싶은데, 방법이 무엇일까요?
DP 문제는 특히, 약간의 생각을 먼저 시도해보는 것이 좋습니다.
물론 문제 분류를 보지 않고 문제를 푸는 연습을 하는 것이 가장 좋지만,
배워가는 입장에선 별 수 있겠습니까 문제 분류라도 보면서 힌트를 좀 얻고... 해야지
1, 2, 4, 3, 5 순서로 아이들이 서 있을 때,
3번 아이를 2번 아이 앞으로 배치하면 1, 2, 3, 4, 5로 정렬된 상태가 됩니다.
2, 4, 1, 3, 5 순서로 아이들이 서 있을 때,
2번 아이를 1번 아이의 뒤로,
4번 아이를 3번 아이의 뒤로 배치하면 1, 2, 3, 4, 5로 정렬된 상태가 됩니다.
최소한으로 옮기고 싶다는 것은,
최대한 정렬된 상태를 유지하면서 옮기고 싶다는 말과 같습니다.
즉, 최대한 "번호가 오름차순인 형태"를 유지하면서 나머지를 옮기는 것입니다.
다시 1, 2, 4, 3, 5에 대해 생각해봅니다.
"1", "2", "4", "5"는 "번호가 오름차순인 부분 수열"로 간주될 수 있습니다.
이 길이는 4이고, 아이들의 수는 5이니, 옮길 수는 5 - 4 = 1이 됩니다.
다시 2, 4, 1, 3, 5에 대해 생각해봅니다.
"2", "4", "5" 또는 "1", "3", "5"는 "번호가 오름차순인 부분 수열"로 간주될 수 있습니다.
이 길이는 3이고, 아이들의 수는 5이니, 옮길 수는 5 - 3 = 2가 됩니다.
즉 이 문제는 가장 긴 증가하는 부분 수열(Longest Increasing Subsequence; LIS)의 길이를 구하는 문제입니다.
(증가하는 부분 수열)을 그대로 둔 상태로, 나머지 원소(아이)를 재배열하면 되기 때문이죠.
따라서 답은 N - LIS가 됩니다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
|
#include <iostream>
using namespace std;
int main(void) {
ios::sync_with_stdio(false);
cin.tie(NULL);
int N;
cin >> N;
int* arr = new int[N];
int* LIS = new int[N];
arr[0] = 0;
for (int i = 0; i < N; i++) {
cin >> arr[i];
LIS[i] = 1;
}
int m = 0;
for (int i = 0; i < N; i++) {
for (int j = 0; j < i; j++) {
if (arr[i] > arr[j]) {
LIS[i] = max(LIS[i], LIS[j] + 1);
m = max(m, LIS[i]);
}
}
}
cout << N - m << "\n";
}
|
cs |
이를 바탕으로 코드로 작성해내면 되겠습니다.
'ps > acmicpc.net' 카테고리의 다른 글
| [C++] boj 17299 오등큰수 (0) | 2022.03.17 |
|---|---|
| [Python 3] boj 2579 계단 오르기 (0) | 2022.02.17 |
[알고리즘] 가장 긴 증가하는 부분 수열(LIS, Longest Increasing Subsequence)
수를 다루는 주제는 과거 전산학과의 유구한 전통과도 같이 다양한 유형을 갖고 있는데,
이번에는 가장 긴 증가하는 부분 수열(Longest Increasing Subsequence; LIS)에 대해 소개해보고자 합니다.
수열은 나열된 수를 말합니다.
규칙을 갖고 있을 수도 있고, 아닐 수도 있는데,
알고리즘에서 말하는 수열은 보통 주어지는 수 입력 자체에는 규칙이 없고,
정해진 주제에 따라 우리가 어떤 '수열' 내지는 '부분 수열'을 구해야 합니다.
이를테면, 주어진 수를 정렬해낸 것도 증가하는, 또는 감소하는 수열을 만들어낸 것이라고 볼 수 있겠지요.
부분 수열은 수열의 일부를 말합니다.
[ 3 7 5 2 6 1 4 ]와 같이 중복된 수가 없다는 조건 외에는 특별한 조건이 없는 수열을 대상으로,
증가하는 부분 수열을 이렇게 찾아볼 수 있습니다.
(3, 7), (3, 5), (3, 5, 6), (3, 6), (3, 4), (5, 6), (2, 6), (2, 4), ...
그러나 결국 문제 출제자가 원하는 것은 어떤 유니크(Unique)한 값입니다.
증가하는 부분 수열의 전체 개수를 세는 것도 문제로 주어질 수 있을지 모르겠지만,
이번에는 '가장 긴 증가하는 부분 수열'을 구해보기로 합니다.
(반대로는 '가장 긴 감소하는 부분 수열'을 구해 볼 수 있음직하다는 생각을 미리 해봅시다.)
가장 긴 증가하는 부분 수열을 구하기 위해서는 다음의 조건이 있습니다.
다음에 추가될 원소는 이전의 원소보다 커야 합니다.
즉, "3"이 포함된 수열에는 "2", "1"을 포함해서는 안됩니다.
LIS를 구하기 위해 첫 번째로 동적 계획법(Dynamic Programming; DP)의 방법을 사용해 볼 수 있습니다.
먼저 각 원소는 길이가 1인 부분 수열로 간주할 수 있으므로, LIS를 1로 초기화합니다.
이 때 LIS[i]는 [i]번째 인덱스의 원소까지를 포함한 증가하는 부분 수열의 길이를 말합니다.
|
1
2
3
4
|
int* LIS = new int[N];
for (int i = 0; i < N; i++) {
LIS[i] = 1;
}
|
cs |
이후 원소간의 비교를 통해 LIS를 구할 것인데,
[j]번 원소가 포함된 부분 수열에 [i]번 원소를 추가한 길이와 현재 길이를 비교합니다.
|
1
2
3
4
5
|
for (int i = 0; i < N; i++) {
for (int j = 0; j < i; j++) {
if (arr[i] > arr[j]) LIS[i] = max(LIS[i], LIS[j] + 1);
}
}
|
cs |
그 중 최댓값을 취해 [i]번 원소가 포함된 부분 수열의 길이를 구합니다.
이 과정에서 얻은 LIS[]의 값들 중 최댓값이 가장 긴 증가하는 부분 수열의 길이입니다.
위 과정은 시간복잡도 O(N^2)인 알고리즘입니다.
즉, 수열의 개수가 10만개라면 알고리즘 문제 해결에 사용할 수 없는 전략이 됩니다.
이를 해결하기 위한 두 번째 방법이 있습니다.
분할정복 기법인 이진탐색(이분탐색)을 활용해 LIS를 구하는 것입니다.
이 아이디어는 정말 신기하고 재밌습니다. 교수들이나 사용할 법한 말투라서 그런지 좀 그렇긴 하네요.
LIS를 선언하되 이번엔 vector를 사용해서 구현해봅니다.
|
1
|
vector<int> LIS;
|
cs |
N개의 원소에 대해 순회할 것인데, 순회 과정에서 마지막 원소보다 큰 원소는 배열에 추가합니다.
큰 원소가 아니라면, LIS 벡터 내부의 원소에 대해 이진탐색을 수행하고 lower bound에 그 원소의 값을 반영합니다.
|
1
2
3
4
5
6
|
vector<int> LIS;
for (int i = 0; i < N; i++) {
if (LIS.empty() || arr[i] > LIS[LIS.size() - 1]) LIS.push_back(arr[i]);
else LIS[lower_bound(LIS.begin(), LIS.end(), arr[i]) - LIS.begin()] = arr[i];
}
|
cs |
결과적으로 LIS가 오름차순으로 만들어지게끔 구성하는 것입니다.
이에 따라 가장 긴 증가하는 부분 수열의 개수는 LIS.size()가 됩니다.
이제 이걸 반대로 하면 가장 긴 감소하는 부분 수열(Longest Decreasing Subsequence)을 만들어 볼 수 있습니다.
'알고리즘 > 알고리즘' 카테고리의 다른 글
| [알고리즘] [C++] 순열(Permutation)과 조합(Combination) (0) | 2022.03.11 |
|---|---|
| [알고리즘] 이진 탐색 / 이분 탐색 (Binary Search) (0) | 2022.02.24 |
| [알고리즘] 재귀(Recursion)와 꼬리 재귀(Tail Recursion) (0) | 2022.02.22 |
| [C++] 입출력 속도 개선, ios::sync_with_stdio(false) (0) | 2022.02.20 |
세그먼트 트리(Segment Tree)와 느린 전파(Lazy Propagation)
트리중에서도 세그먼트 트리(Segment Tree)는 구간 사이의 연산을 효율적으로 할 수 있도록 도와주는 자료구조입니다.
어떤 임의의 배열에서, 특정 인덱스의 값이 계속해서 변하는데,
동시에 어떤 구간 [a, b]까지의 값을 모두 더한 값을 얻고자 한다면 어떻게 해야할까요?
일반적인 방법으로 시도한다면,
주어진대로 배열의 값을 변경하고, 합을 새로 구해야 할 것입니다.

어떤 배열 [1, 7, 3, 2, 4, 6]에 대해서, 구간 [1, 4]의 합은 1 + 7 + 3 + 2 = 13이 될 것입니다.
(인덱스는 1부터 시작한다고 가정합니다.)
4번 인덱스의 값을 "8"로 바꾸고, 구간 [1, 4]의 합을 구하면 어떻게 될까요?

1 + 7 + 3 + 8 = 19가 될 것입니다.
어떤 주어진 배열이 있고, 구간에 대한 합을 구하려고 할 때
우리는 구간합(Prefix sum)의 원리를 사용할 수 있음을 알고 있습니다.
어떤 N개의 원소를 가진 배열 arr[]이 있다고 할 때,
주어지는 구간 [a, b]에 대해 이 배열의 원소들의 합을 구하려면,
누적합을 먼저 계산한 배열 sum[]을 이용해 다음과 같이 계산할 수 있습니다.
|
1
|
int ret = sum[b] - sum[a] + arr[a];
|
cs |
sum[b]는 [0, b]까지의 모든 값을 더한 값을 가지고 있고,
sum[a]는 [0, a]까지의 모든 값을 더한 값을 가지고 있으므로,
sum[b]에서 sum[a]를 빼면 [a - 1, b]까지의 모든 값을 더한 값이 되고,
arr[a]를 여기에 더하면 [a, b]까지의 모든 값을 더한 값이 되기 때문입니다.
그런데... 구간합(Prefix sum)의 원리를 위와 같은 문제에 적용하기는 쉽지 않습니다.
특정 인덱스의 값을 바꾸거나, 특정 구간의 값을 바꾸는 과정에서,
새로이 sum 배열의 값을 하나하나 바꾸어주어야 하고 이는 필연적으로 알고리즘의 수행 시간을 늘리기 때문입니다.
배열의 크기가 100 이하로 작은 편이라면 큰 시간 소모 없이 답을 구해낼 수 있겠지만,
배열의 크기가 1만, 10만 정도로 큰 편이라면 너무나도 많은 시간을 소모해야 합니다.
따라서 새로운 방법을 고찰할 필요가 있습니다. 그 방법이 바로 세그먼트 트리(Segment Tree)를 이용하는 것입니다.
세그먼트 트리는 그 이름과 같이, 구간을 부분부분 나눠(Segment) 트리를 구성합니다.
배열을 구간별로 나눠 그 합을 미리 저장해두고, 구간 [a, b]에 대한 쿼리(query)가 발생할 때마다 이 구간들에 대한 합을 구해서 반환한다면 연산시간이 매우 줄어듭니다.

위는 원소 4개로 구성된 세그먼트 트리의 예시입니다.
[a-b]는 이 노드(Node)가 대표하고 있는 구간을 의미하고,
구간 아래의 숫자는 이 노드의 트리상 인덱스를 의미합니다.
이런 형태로 각 노드가 자신이 대표하는 구간의 구간합을 미리 계산해둔 상태로 저장하고 있다면,
구간 [1, 4]에 대한 연산은 Tree[1]을 반환하면 될 것입니다.
Tree[1]이 arr[1]부터 arr[4]까지의 합을 저장하고 있기 때문입니다.
그러면 전체 구간이 아닌 구간의 합을 구하고자 한다면 어떨까요?

구간 [2, 4]에 대한 연산은 Tree[5]와 Tree[3]의 합을 반환하면 됩니다.
Tree[5]는 arr[2]의 값을 저장하고 있으며,
Tree[3]은 arr[3]과 arr[4]의 합을 저장하고 있기 때문입니다.
그렇다면 이렇게 구간별로 나뉜, 합을 계산한 트리를 만드는 방법을 생각해봅시다.
전체 구간 [1, N]을 대표하는 노드 tree[1]가,
그 구간을 좌 우로 나누고 나뉜 구간을 대표하는 자식을 갖도록 설정해야 합니다.
즉, tree[1]은 tree[2] + tree[3]의 값으로,
tree[2]는 tree[4] + tree[5]의 값으로,
tree[3]은 tree[6] + tree[7]의 값으로 구성되도록 하는 트리를 만들어야 합니다.
그 함수를 init라고 합시다.
init함수는 세 개의 인수가 필요합니다.
현재 조회중인 노드의 번호인 node,
탐색중인 구간 범위의 가장 왼쪽을 가리킬 left,
탐색중인 구간 범위의 가장 오른쪽을 가리킬 right입니다.
이 함수가 자식을 호출하는 과정에서 left와 right가 일치하는 순간(left == right)이 있을 것입니다.
이 때의 node인덱스에 arr[left]의 값을 저장하고, 이를 반환해야 합니다.
|
1
|
if (left == right) return tree[node] = arr[left];
|
cs |
left와 right가 일치하지 않을 때에는 재귀적으로 자기자신을 호출하며 부모 노드의 값에 자식 노드의 합을 저장합니다.
|
1
2
3
4
5
|
int init(int node, int left, int right) {
if (left == right) return tree[node] = arr[left];
int mid = (left + right) / 2;
return tree[node] = init(node * 2, left, mid) + init(node * 2 + 1, mid + 1, right);
}
|
cs |
이제 우리는 구간 합을 노드로 가지는 트리를 분할정복(Devide and Conquer)의 방식으로 완성했습니다.
값을 알고 있다면, 이제 구간 합을 구할 수 있어야 합니다.
이렇게 저장된 값을 조회하기 위해 query라는 함수를 작성해보고자 합니다.
query함수는 다섯개의 인수를 가지게 됩니다.
현재 조회중인 노드의 번호인 node,
탐색중인 구간 범위의 가장 왼쪽을 가리킬 left,
탐색중인 구간 범위의 가장 오른쪽을 가리킬 right,
조회할 구간 [a, b]에서의 a,
조회할 구간 [a, b]에서의 b입니다.
구간 [a, b]의 합을 구하는 과정에서 left, right는 어떤 역할을 해야 할까요?
어떤 구간 [a, b]의 합을 구하기 위해 우리는 query함수를 이렇게 호출해야 합니다.
|
1
|
query(1, 1, N, a, b);
|
cs |
첫 노드는 1번이며, 이 노드는 [1, N]을 대표하고 있고, [a, b]의 구간합을 구해야 하기 때문입니다.
각 노드의 자식은 구간 [left, right]를 기준으로 두 구간으로 나뉘게 됩니다.

Tree[1]은 Tree[2]와 Tree[3]을 자식으로 가졌는데,
Tree[1]이 [1, 4]를 대표하고, Tree[2]는 [1, 2]를 대표하며, Tree[3]은 [3, 4]를 대표하고 있습니다.
즉, 부모의 구간인 [1, 4]를 두 구간으로 나눠 그 자식의 구간이 결정된 것입니다.
다시 구간 [a, b]의 합을 구하는 과정에서 left, right의 역할을 생각해봅시다.
내가 구하고자 하는 구간합은 [1, 3]인데, 그렇다면?
[1, 4]의 왼쪽 자식인 [1, 2]를 더하고, [1, 4]의 오른쪽 자식인 [3, 4]의 왼쪽 자식인 [3]을 더하면 됩니다.
이 과정에서 [1, 4]의 오른쪽 자식인 [3, 4]의 오른쪽 자식인 [4]는 무시해야 합니다.
이를 일반화해서, 구간 [a, b]에 포함되지 않는, 왼쪽 값과 오른쪽 값은 무시해야 합니다.
따라서 첫번째 조건은 결정했습니다.
|
1
|
if (b < left || a > right) return 0;
|
cs |
내가 더해야 할 값은 [a ≤ left ≤ right ≤ b]인 관계를 갖고 있어야 하기 때문입니다.
그리고, 이 관계를 가진 상황에는 자신의 값을 반환하면 됩니다.
|
1
2
|
if (b < left || a > right) return 0;
if (left >= a && right <= b) return tree[node];
|
cs |
마지막으로, 이 함수가 재귀적으로 왼쪽 및 오른쪽 자식을 호출할 수 있어야 합니다.
|
1
2
3
4
5
6
|
int query(int node, int left, int right, int a, int b) {
if (b < left || a > right) return 0;
if (left >= a && right <= b) return tree[node];
int mid = (left + right) / 2;
return query(node * 2, left, mid, a, b) + query(node * 2 + 1, mid + 1, right, a, b);
}
|
cs |
구간 [1, 3]의 합을 구하는 과정은 다음과 같습니다.
query(1, 1, 4, 1, 3)
= query(2, 1, 2, 1, 3) + query(3, 3, 4, 1, 3)
= tree[2] + query(6, 3, 3, 1, 3) + query(7, 4, 4, 1, 3)
= tree[2] + tree[6] + 0
query(2, 1, 2, 1, 3)은 left(1)이 a(1) 이상이고, right(2)가 b(3) 이하이므로 tree[2]를 반환합니다.
query(6, 3, 3, 1, 3)은 left(3)이 a(1) 이상이고, right(3)가 b(3) 이하이므로 tree[6]을 반환합니다.
query(7, 4, 4, 1, 3)은 b(3)가 left(4)보다 작으므로 0을 반환합니다.
그렇다면 이제 임의의 구간 [a, b]에 대해 합을 구할 수 있겠습니다. 문제는, 거기서 그치면 안 된다는 점이죠.
특정한 인덱스(또는 구간)에 대해 값이 변경될 경우에도 구간합을 구할 수 있을까?
이 문제에 답하기 위해 update라는 함수를 생각해봅시다.
어떤 인덱스의 값을 변경한다면, tree의 값도 자연스레 바뀌어야 할 것입니다.
이것도 bottom-up 방식의 재귀함수로 이 과정을 생각해본다면,
arr[3]이 변경되면 구간 [3]을 대표하는 노드가 바뀌어야 할 것이고,
구간 [3, 4]를 대표하는 노드가 바뀌어야 할 것이고,
구간 [1, 4]를 대표하는 노드가 바뀌어야 할 것입니다.
이 역할을 수행하는 update함수를 만들어봅시다.
update 함수를 구성하기 위해 필요한 인수를 생각해봅니다.
현재 조회중인 노드 번호인 Node,
탐색중인 구간 범위의 가장 왼쪽을 가리킬 left,
탐색중인 구간 범위의 가장 오른쪽을 가리킬 right,
변경할 인덱스를 가리킬 idx,
변경할 값을 가리킬 value가 필요합니다.

arr[3]의 값을 변경할 때, [1, 4]를 대표하는 노드와 [3, 4]를 대표하는 노드는 바뀌겠지만,
[1, 2]를 대표하는 노드는 영향을 받지 않아야 합니다.

idx와 left, right의 관계를 생각해보면,
idx가 left보다 작거나, idx가 right보다 크면 변경할 필요가 없음을 생각할 수 있습니다.
그런데 이 때, 0을 반환하는 것이 아니라 tree[node]를 반환해야 합니다.
|
1
|
if (idx < left || idx > right) return tree[node];
|
cs |
이유는 곰곰이 생각해보면 알 수 있습니다.
이 역시 [부모 노드의 값] = [왼쪽 자식 노드의 값] + [오른쪽 자식 노드의 값]으로 계산할텐데,
arr[3]을 변경하는 과정에서 [1, 2] 구간의 값을 0으로 반환해버리면,
[1, 4] 구간의 값은 [3, 4] 구간의 값만을 반영하게 될 것입니다.
심지어, [4, 4] 구간의 값도 0으로 반환될테니, (idx = 3, left = right = 4)
구간 [1, 4]을 대표하는 노드의 값이 그저 arr[3]이 되겠지요.
따라서, 내가 원하는 범위가 아니더라도 이 노드가 대표하는 값 tree[node]를 반환해주어야 합니다.
update 과정에서도 left와 right가 일치하는 경우, 즉 말단 노드(leaf node)에 도달하는 경우에는 이 값을 갱신해주어야 합니다.
따라서 다음 조건은 이렇게 작성할 수 있습니다.
|
1
2
|
if (idx < left || idx > right) return tree[node];
if (left == right) return tree[node] = value;
|
cs |
이제 마지막으로, 부모 노드의 값이 자식 노드의 합이 되도록 함수를 작성합니다.
|
1
2
3
4
5
6
|
int update(int node, int left, int right, int idx, int value) {
if (idx < left || idx > right) return tree[node];
if (left == right) return tree[node] = value;
int mid = (left + right) / 2;
return tree[node] = update(node * 2, left, mid, idx, value) + update(node * 2 + 1, mid + 1, right, idx, value);
}
|
cs |
이제 세그먼트 트리를 구성하고, 특정 인덱스에 변화가 일어나더라도 특정 구간 [a, b]의 합을 구할 수 있게 되었습니다.
여기까지의 전체 코드는 다음과 같습니다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
|
#include <iostream>
#include <vector>
using namespace std;
vector<int> arr;
vector<int> tree;
int init(int node, int left, int right) {
if (left == right) return tree[node] = arr[left];
int mid = (left + right) / 2;
else return tree[node] = init(node * 2, left, mid) + init(node * 2 + 1, mid + 1, right);
}
int update(int node, int left, int right, int idx, int value) {
if (idx < left || idx > right) return tree[node];
if (left == right) return tree[node] = value;
int mid = (left + right) / 2;
return tree[node] = update(node * 2, left, mid, idx, value) + update(node * 2 + 1, mid + 1, right, idx, value);
}
int update(int node, int left, int right, int idx, int value) {
if (idx < left || idx > right) return tree[node];
if (left == right) return tree[node] = value;
int mid = (left + right) / 2;
return tree[node] = update(node * 2, left, mid, idx, value) + update(node * 2 + 1, mid + 1, right, idx, value);
}
int main(void) {
int N;
cin >> N;
arr = vector<int>(N + 1);
tree = vector<int>(N * 4);
for (int i = 1; i <= N; i++) {
cin >> arr[i];
}
init(1, 1, N);
}
|
cs |
그런데 여기까지만 해서는 질문에 답할 수 없습니다!
특정한 인덱스(또는 구간)에 대해 값이 변경될 경우에도 구간합을 구할 수 있을까?
구간에 대한 변경을 처리한다고 생각해봅니다.
100만개의 배열을 대상으로 [2, 999999]와 같은 큼지막한 구간에 4를 더하고, [1, 888844]에는 -2를 더하고, ... 이를 반복하면 반드시 시간초과가 발생할 것입니다.
이 상태로는 update함수가 구간의 모든 인덱스를 대상으로 사용되어야 하기 때문입니다.
그래서 우리는 "느리게 전파되는(Lazy Propagation) 세그먼트 트리"를 만들 수 있어야 합니다.

기존의 4원소 배열로부터 구성된 세그먼트 트리를 다시 봅니다.
이 때, 위에서와는 다르게 텍스트를 조금 바꿨습니다.
배열의 원소가 [1, 7, 4, 2]라고 가정한 것이죠.
위는 [구간], 아래는 구간합을 표현했습니다.
구간 [1, 3]에 대해 3을 더한 뒤, 구간 [1, 3]을 조회하려면?
구간 [1, 2]에 6을 더하고, 구간 [3, 3]에 3을 더하면 될 것 같습니다.
물론 언젠가 구간 [1, 1]을 조회할지도 모르니, 구간 [1, 1]에도 3이 더해지긴 해야 합니다.
바로 여기서 느린 전파(Lazy Propagation)를 사용합니다.
어떤 구간 [a, b]에 대해서 값 [value]를 더해줄 것임을 예고해줄 새 벡터 배열 lazy를 선언합니다.
|
1
2
3
|
vector<int> arr;
vector<int> tree;
vector<int> lazy;
|
cs |
루트 노드인 [1, 4] 노드와 구간 [1, 3]을 비교해, 겹치는 구간만큼 값을 더해주고, 자손에게 lazy를 전파합니다.
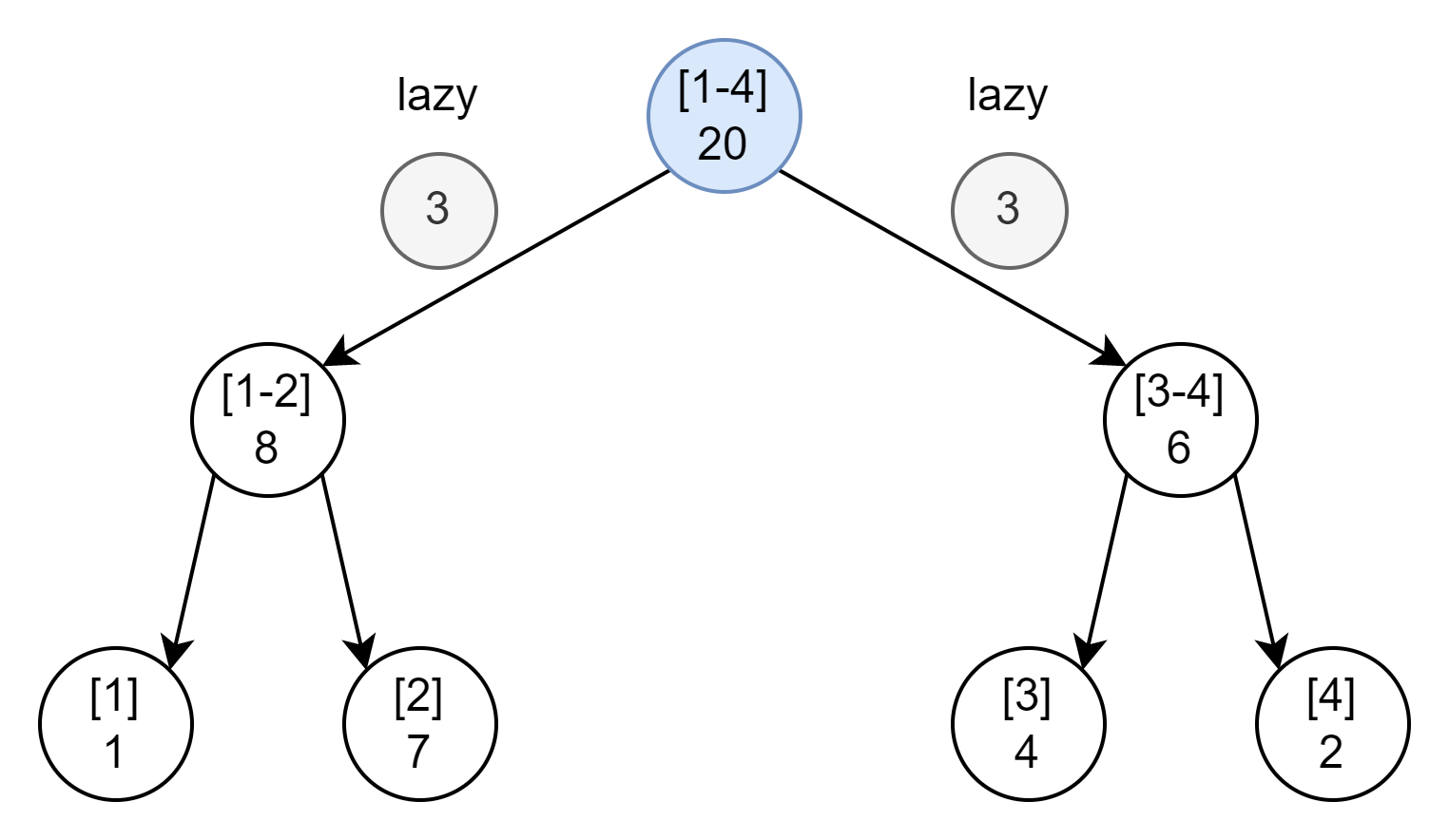
[1, 2] 노드는 구간 [1, 3]의 일부이니, 겹치는 구간만큼 값을 더하고 lazy를 자손에게 전파합니다.

[3, 4] 노드와 구간 [1, 3]의 겹치는 구간만큼 값을 더하고 lazy를 자손에게 전파합니다.
그런데 이 때, [4] 노드는 [1, 3] 구간과 겹치지 않으므로 lazy가 전파되지 않습니다.

전달된 lazy는 아직 더해지지 않은 상태로 있다가, 자손에 대한 update가 재귀로 발생하거나 query가 수행되면서 점진적으로 더해집니다.

즉, 요지는 구간합을 반영할 새 벡터 lazy를 만들고, 이를 "필요할 때마다" 연산하는 데에 있습니다.
구간합을 반영하기 위한 새 update함수를 작성합니다.
이 함수는 먼저 현재 노드가 반영해야 할 lazy가 있는지를 검사해야 합니다.
lazy가 있을 경우 이를 자신에게 반영하고, 자손에게 전파합니다.
|
1
2
3
4
5
6
7
8
9
|
if (lazy[node] != 0) {
tree[node] += lazy[node] * (right - left + 1);
if (left != right) {
lazy[node * 2] += lazy[node];
lazy[node * 2 + 1] += lazy[node];
}
lazy[node] = 0;
}
|
cs |
자신이 leaf 노드가 아닌지를 검사한 뒤(if left != right) 자손에게 전파해야겠죠.
이 함수는 인수로 idx가 아닌 a, b를 사용할 것입니다.
(node, left, right, a, b, value)
이상적인 업데이트 반영은 [a ≤ left ≤ right ≤ b]일 때인데,
[ a b left right ] 또는 [ left right a b ]일 때는 연산하지 않아야 합니다.
|
1
|
if (left > b || right < a) return;
|
cs |
그리고, 이상적인 구간에 속할 때 ([a ≤ left ≤ right ≤ b]일 때)에는 현재 노드에 구간합을 반영하고 자손에 lazy를 전파합니다.
|
1
2
3
4
5
6
7
8
9
|
if (left >= a && right <= b) {
tree[node] += value * (right - left + 1);
if (left != right) {
lazy[node * 2] += value;
lazy[node * 2 + 1] += value;
}
return;
}
|
cs |
마지막으로 좌, 우 자식에 대해 update함수를 재귀적으로 호출하고, 현재 노드에 그 값을 반영합니다.
|
1
2
3
|
update(node * 2, left, (left + right) / 2, a, b, value);
update(node * 2 + 1, (left + right) / 2 + 1, right, a, b, value);
tree[node] = tree[node * 2] + tree[node * 2 + 1];
|
cs |
이로서 update함수를 완성했습니다. 전체 코드는 다음과 같습니다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
|
void update(int node, int left, int right, int a, int b, int value) {
if (lazy[node] != 0) {
tree[node] += lazy[node] * (right - left + 1);
if (left != right) {
lazy[node * 2] += lazy[node];
lazy[node * 2 + 1] += lazy[node];
}
lazy[node] = 0;
}
if (left > b || right < a) return;
if (left >= a && right <= b) {
tree[node] += value * (right - left + 1);
if (left != right) {
lazy[node * 2] += value;
lazy[node * 2 + 1] += value;
}
return;
}
int mid = (left + right) / 2;
update(node * 2, left, mid, a, b, value);
update(node * 2 + 1, mid + 1, right, a, b, value);
tree[node] = tree[node * 2] + tree[node * 2 + 1];
}
|
cs |
update 함수는 바꾸었는데, 이제 query함수를 바꾸어야 합니다.
(물론, init 함수를 바꿀 필요는 없습니다.)
query함수 역시 lazy가 존재할 경우 현재 노드에 반영하고, 자손에 이를 전파하기만 하면 됩니다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
int query(int node, int left, int right, int a, int b) {
if (lazy[node] != 0) {
tree[node] += lazy[node] * (right - left + 1);
if (left != right) {
lazy[node * 2] += lazy[node];
lazy[node * 2 + 1] += lazy[node];
}
lazy[node] = 0;
}
int mid = (left + right) / 2;
if (left > b || right < a) return 0;
if (left >= a && right <= b) return tree[node];
return query(node * 2, left, mid, a, b) + query(node * 2 + 1, mid + 1, right, a, b);
}
|
cs |
이제 주어진 질문에 답할 수 있습니다.
특정한 인덱스의 값이 변경될 때에 대한 연산을 수행하기 위해 세그먼트 트리를 사용하였고,
특정한 구간의 값이 변경될 때에 대한 연산을 수행하기 위해 느리게 전파되는 세그먼트 트리를 사용했습니다.
'알고리즘 > 자료구조' 카테고리의 다른 글
| 힙(Heap)과 최대 힙(Max Heap), 최소 힙(Min Heap) (0) | 2022.02.20 |
|---|